Định nghĩa và công thức cấp số cộng chính xác nhất

Trong các kỳ thi quan trọng, cấp số cộng luôn là vấn đề Toán học thường xuyên được xuất hiện. Tuy nhiên thực tế cho thấy, không ít học sinh vẫn chưa nắm rõ công thức cấp số cộng và cách giải quyết các dạng bài tập liên quan tới mảng kiến thức này. Do đó trong bài viết ngày hôm nay, ReviewAZ sẽ đồng hành cùng những bạn mất gốc, đi tìm hiểu về cấp số cộng nhé!

Định nghĩa công thức cấp số cộng

Trong môn Toán học, cấp số cộng được nhắc tới để chỉ một dãy số, với điều kiện: số đứng sau bằng tổng của số đứng trước với một số không đổi. Số không đổi này còn có tên gọi khác là công sai. Một cấp số sẽ có thể chạy vô hạn hoặc hữu hạn. Ví dụ cụ thể: 3, 5, 7, 9,..

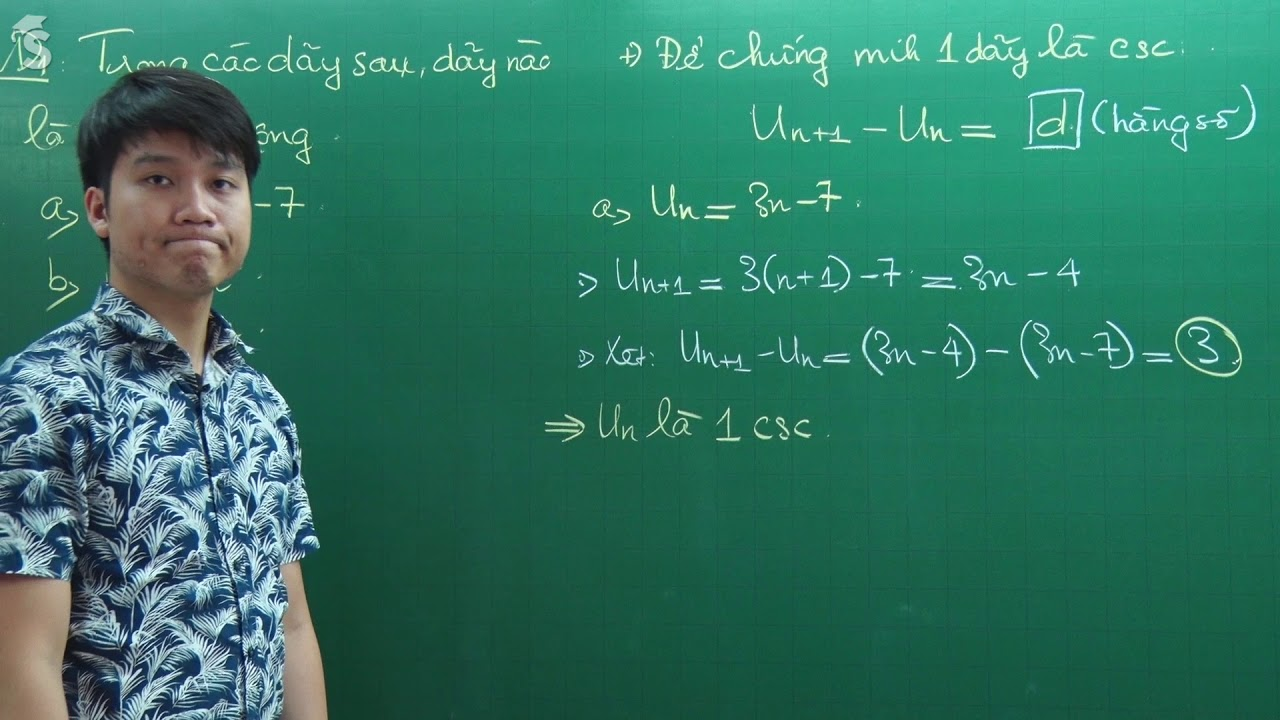
Cấp số cộng sẽ ở dạng: a2 – a1 = a3 – a2 = … = an – an-1 = d

Trong đó:

• a1 là số hạng đầu tiên
• an là số hạng cuối cùng
• ak là số hạng thứ k nằm trong cấp số cộng
• n là số hạng thứ cấp
• d là công sai cấp số cộng

Ngoài ra còn có các trường hợp khác:

• Cấp số cộng thể hiện tính chất qua đẳng thức: ak+1 – 2ak + ak-1 = 0 với mọi giá trị k=2, …, n-1
• Hay ak= ½ (ak-1+ ak+ 1), số giữa bằng trung bình hai số đứng cạnh
• Cấp số cộng có hữu hạn phân tử

Có thể bạn quan tâm: Cách tính diện tích hình thang giúp cho việc học tập trở nên thuận lợi

Công thức cấp số cộng chính xác cho mọi bài toán

Để giải các bài toán liên quan tới cấp số cộng, bạn cần nắm chắc được công thức về số hạng tổng quát, tính chất và các công thức liên quan. Điều này vô cùng quan trọng, là chìa khóa giúp bạn chinh phục mọi bài toán từ dễ tới khó.

Số hạng tổng quát

Dựa vào số hạng đầu và công sai, ta có thể tính được số hạng tổng quát.

• Công thức tính như sau:  un = u1 + (n – 1)d, (trong đó n2)
• Ví dụ:

Cho một cấp số cộng có ký hiệu là  (un) biết được u1 = -1 và  d = 3. Hãy tìm u21.

Áp dụng công thức, ta có:  

u20 = u1 + (21 – 1)d

       = u1 + 20d

        = -1 + 20×3

        =59

Công thức tính chất cấp số cộng

• Để tìm tính chất- đặc điểm cấp số cộng, ta cần áp dụng công thức:

uk= uk- 1+ uk+1 / 2

Trong đó: k2 hoặc uk+1+uk-1= 2uk.

• Ví dụ cụ thể:

Ta có 3 số lần lượt là 9; x; 13. Yêu cầu: lập một cấp số cộng và tìm X

Áp dụng công thức, ta có phương trình:  x= 9+132= 11

Như vậy suy ra:  x = 11 và cấp số cộng cần tìm là 9, 11, 13.

Tính tổng n số hạng đầu:

• Công thức:

Sn= n(u1+u2)/2, điều kiện là n thuộc tập hợp N*

 Sn= nu1+ n(n-1)/2 *d

Sn= n[2u1+ (n-1)d]/2

• Ví dụ cụ thể: Ta có cấp số cộng (un) với điều kiện thỏa mãn: u1=-1, d=3. Bạn hãy thực hiện tính S20

Áp dụng công thức, ta có:

S20=20u1+20.(20-12).d

      = 20.(-1) + 20.192. 3

      = 550

Có thể bạn quan tâm: Cách tính chu vi hình tròn và các bài tập ví dụ về tính chu vi hình tròn

Các dạng bài tập về công thức cấp số cộng và cách giải

Điều khó nhất của cấp số cộng không phải nằm ở công thức, mà chính là hành trình đi tìm ra đáp số cuối cùng. Khi làm Toán, sẽ có một số dạng bài bạn thường xuyên gặp phải. Nếu bạn thực hành đều đặn thì sẽ hoàn toàn không khó để chinh phục và lấy điểm cao.

Dạng 1: Nhận biết về cấp số cộng

• Yêu cầu: Tìm cấp số cộng trong các dãy số đã cho sẵn
• Cách thực hiện:

• Bước 1: Tìm công sai của dãy khi đã được biết hai số hạng liên tiếp, liền kề nhau theo công thức: d=un–un–1,∀n≥2.
• Bước 2: Đưa ra kết luận: Nếu d là một số không đổi thì dãy (un) là cấp số cộng. Ngược lại, nếu d thay đổi và chạy theo n thì dãy (un) không đáp ứng yêu cầu là cấp số cộng.

Dạng 2: Tìm công sai ẩn số bằng công thức cấp số cộng

• Bạn hoàn toàn có thể sử dụng các tính chất của cấp số cộng ở trên. Tuy nhiên cần biến đổi để tính công sai d dễ dàng nhất

Dạng 3: Tìm số hạng của cấp số cộng

• Xử lý dạng bài này bằng cách ứng dụng công thức tính số hạng tổng quát un=u1+(n–1)d

Dạng 4: Tính tổng cấp số cộng của n số hạng đầu tiên

Để làm dạng bài này, bạn hãy vận dụng công thức tính tổng cấp số cộng như sau

Sn=u1+u2+…+un=(u1+un).n2=[2u1+(n–1)d].n2

Dạng 5: Tìm cấp số cộng

Đây là dạng quen thuộc và phổ biến nhất, thường bắt gặp trong các đề thi cấp 3 và Đại học. Tuy cũng là dạng nâng cao, nhưng bạn hoàn toàn có thể xử lý bằng cách:

• Đọc đề và tìm kiếm các yếu tố xác định một cấp số cộng như: số hạng đầu u1, công sai, số hạng cuối
• Áp dụng công thức cho số hạng tổng quát un=u1+(n–1)d

Trên đây là những thông tin bạn nên biết về công thức cấp số cộng, hãy áp dụng để trau dồi kiến thức và học tốt môn Toán hơn. Hy vọng bài viết đã giúp ích cho bạn. Đừng quên theo dõi thêm các cập nhật mới từ ReviewAZ nhé!

Có thể bạn quan tâm: Cấp số nhân là gì? Định nghĩa, công thức và bài tập ứng dụng