Định lý talet là gì? Ứng dụng định lý Talet vào toán học như thế nào?

Định lý Pitago hay định lý định lý Fermat đã vô cùng quen thuộc trong lĩnh vực toán học rồi. Nhưng bạn đã từng nghe đến định lý Talet chưa? Đây là một định lý đóng vai trò rất quan trọng trong hình học về tỷ lệ giữa các đoạn thẳng. Để bạn đọc có thể nắm rõ cụ thể về những kiến thức liên quan đến chủ đề này, chúng tôi sẽ đưa ra thông tin dưới đây.

Định lý Talet là gì?

Trước khi hiểu về định lý Talet chúng ta cần nhắc đến tỉ số của hai đoạn thẳng. Đây là yếu tố cần có và phải nắm rõ để có thể hiểu được hết ý nghĩa của định lý Talet. Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo. Tỉ số này không bị phụ thuộc vào cách chọn đơn vị đo.

Nhà toán học Thales là cha đẻ của định lý này. Ông sống trong khoảng thời gian 624 TCN - 546 TCN. Ông đã có đóng góp 6 định lý về hình học như tính chất về góc, tam giác cân, đường tròn và tỷ lệ đoạn thẳng.

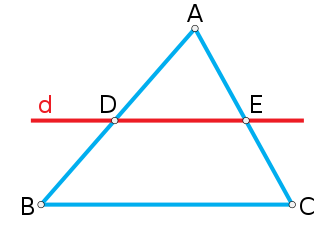
Định lý Talet thuận trong tam giác

Định lý Talet thuận trong tam giác như sau: “Nếu có một đường thẳng cắt hai cạnh của một tam giác và song song với hai cạnh còn lại thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.”

Ví dụ: Cho tam giác ABC với đường thẳng e cắt đoạn thẳng AB tại điểm D, cắt đoạn thẳng AC tại điểm E và song song với đoạn thẳng BC. Từ định lý Talet thuận trong tam giác có thể suy ra được DE song song với BC.

Định lý Talet đảo trong tam giác

Định lý Talet đảo trong tam giác như sau: “Nếu có một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với hai cạnh còn lại của tam giác.”

Cần chú ý định lý này vẫn đúng cho các trường hợp đường thẳng cắt phần kéo dài của hai cạnh trong tam giác đó. Giả sử trên hai đường thẳng a và b lần lượt lấy hai bộ ba điểm (A, B, C) và (A', B', C') sao cho AB/A'B'= BC/B'C' = CA/C'A'

Từ định lý Talet đảo trong tam giác ta có thể biết, ba đường thẳng AA', BB', CC' cùng song song với một mặt phẳng, nghĩa là ba đường thẳng đó nằm trên ba mặt phẳng song song với nhau.

Định lý Talet trong hình thang và trong không gian

Định lý Talet trong hình thang được định luật như sau: “Nếu có một đường thẳng song song với 2 cạnh đáy của hình thang và cắt 2 cạnh bên của hình thang thì nó sẽ định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.”

Định lý Talet trong không gian được định luật như sau: “Ba mặt phẳng song song chắc chắn trên hai đường thẳng những đoạn thẳng tỉ lệ”

Có thể bạn quan tâm: Diện tích hình tròn là gì? Có những công thức nào để tính?

Hệ quả của định lý Talet như thế nào?

Trong toán học, định lý Talet có 3 hệ quả với một hệ quả mở rộng. Bạn đọc cần nắm rõ các hệ quả để giải quyết được các bài tập một cách dễ dàng hơn.

• Hệ quả 1: Nếu Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có 3 cạnh tương ứng tỉ lệ với 3 cạnh tam giác đã cho
• Hệ quả 2: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu
• Hệ quả 3 – Talet mở rộng: Nếu 3 đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tương ứng tỉ lệ.

Có thể bạn quan tâm: Cách tính diện tích hình thang giúp cho việc học tập trở nên thuận lợi

Ứng dụng định lý Talet trong những dạng toán nào?

Trong toán học định lý Talet được áp dụng với nhiều dạng bài toán khác nhau. Trong đó các dạng bài về tính chu vi của đoạn thẳng, hình học hoặc chứng minh các đường thẳng song song.

Cụ thể như sau:

• Dạng 1: Tính độ dài của đoạn thẳng, chu vi, diện tích và các tỉ số của bài toán. Các dạng giải bài tập kiểu này sẽ thường được áp dụng thêm định lý Talet vào, hệ quả của định lý và tỉ số đoạn thẳng. Về định lý, nếu một đường thẳng nó song song với một cảnh của tam giacs và cắt hai cạnh còn lại thì sẽ có thể định ra những đoạn thẳng tương ứng tỉ lệ.
• Dạng 2: Dùng định lý Talet để chứng minh các đường thẳng song song và chứng minh đẳng thức trong hình học. Có thể sử dụng định lý Talet thuận, định lý Talet đảo và hệ quả của định lý Talet trong trường hợp này.

Như vậy chúng tôi đã cung cấp đầy đủ thông tin có liên quan đến định lý Talet qua bài viết trên. Hy vọng rằng chia sẻ đó giúp bạn nắm rõ được kiến thức toán học về chủ đề này. Hãy tiếp tục theo dõi thêm nhiều bài viết mới tại web ReviewAZ nhé

Có thể bạn quan tâm: Cách tính chu vi hình tròn và các bài tập ví dụ về tính chu vi hình tròn