Các thông tin liên quan về dạng toán hàm số liên tục

Trong toán học lớp 11, kiến thức về hàm số liên tục được nhắc đến khá nhiều. Đây được coi là dạng toán phức tạp, có nhiều dạng bài nhỏ trong đó. Điều này đòi hỏi người học cũng như người dạy phải nắm chắc kiến thức và có vốn phông nền tốt. Vì thế, bài viết dưới đây ReviewAZ sẽ gợi ý cho bạn những kiến thức về hàm số liên tục. Hy vọng có thể giúp bạn giải các bài toán liên quan nhanh chóng và chính xác.

Lý thuyết về hàm số liên tục

Đầu tiên, để có thể giải các bài toán về dạng toán này, người học cần nắm chắc các khái niệm, lý thuyết liên quan về hàm số liên tục. Việc này sẽ đem lại kiến thức nền chắc, người học có thể phân biệt được các vùng kiến thức khác nhau.

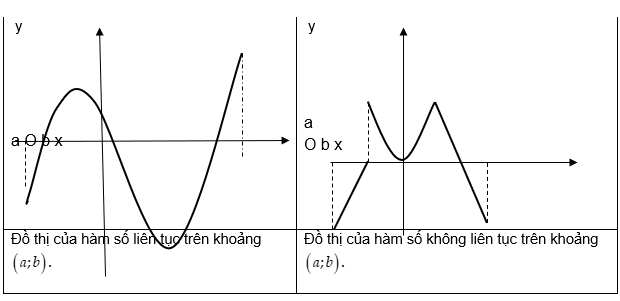
Định nghĩa hàm số liên tục

Một hàm số y = f (x) và được xác định trên khoảng K, với x0 thuộc K. Khi đó, hàm số ban đầu được gọi là hàm số liên tục tại điểm x0 nếu lim

x→x0

f(x)=f(x0).

Trong đó:

• Hàm số y = f (x) nếu không liên tục tại điểm x0 thì được gọi làm hàm số gián đoạn tại điểm x0.
• Hàm số y = f (x) liên tục trên khoảng cho trước thì được gọi là hàm số liên tục tại mọi điểm thuộc khoảng cho trước ban đầu.
• Hàm số y = f (x) liên tục trên khoảng [a, b] thì được gọi là hàm số liên tục từ khoảng a đến khoảng b.
• Đồ thị hàm số của hàm số liên tục sẽ là một đường kẻ liền trên khoảng cho trước ban đầu.

Có thể bạn quan tâm: Cách tính chu vi hình tròn và các bài tập ví dụ về tính chu vi hình tròn

Định lý về hàm số liên tục

Hàm số liên tục tồn tại 3 định lý như sau:

Định lý 1:

Hàm số đa thức được gọi là hàm số liên tục bởi chúng liên tục trên toàn bộ tập số thực R.

Hàm số phân thức hữu tỉ (là thương của hai đa thức bất kỳ) và các hàm số lượng giác liên tục trên mỗi khoảng của tập xác định ban đầu.

Định lý 2:

Cho hai hàm số ban đầu là y = f (x) và y = g (x). Hai hàm số này liên tục tại điểm x0, khi đó ta có các kết quả như sau:

Các hàm số y = f (x) + g (x), y = f (x) – g (x) và y = f (x) . g (x) liên tục tại điểm x ban đầu.

Hàm số y = f (x) / g (x) với điều kiện g (x0) khác 0 sẽ được gọi là liên tục tại điểm x0.

Định lý 3:

Nếu hàm số cho trước y = f (x) liên tục trên đoạn bất kỳ [a, b] và f (a) . f (b) < 0 thì chứng minh được rằng tồn tại ít nhất một điểm c thuộc khoảng (a, b) với điều kiện f (c) = 0.

Lưu ý: định lý 3 thường được sử dụng trong các trường hợp để chứng minh sự tồn tại của các nghiệm phương trình trên một khoảng.

Có thể bạn quan tâm: Thừa số là gì? Làm sao để phân tích một số thành các thừa số nguyên tố

Một số dạng toán thường gặp của hàm số liên tục

Trong bài viết này, chúng tôi sẽ chỉ ra cho bạn 3 dạng cơ bản của hàm số liên tục. Hy vọng bạn có thể áp dụng để giải các bài toán liên quan dễ dàng và nhanh chóng nhất.

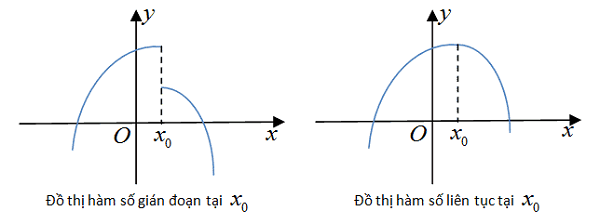
Dạng 1: Hàm số liên tục tại 1 điểm

Đây là dạng toán cơ bản và được coi là đơn giản nhất của kiến thức về dạng toán hàm số liên tục. Theo đó, ta thừa nhận công thức sau:

Hàm số f (x) liên tục tại điểm a cho trước khi và chỉ khi lim (x => a) f (x) = f (a).

Khi thừa nhận công thức trên, chúng ta sẽ phải có một số điều kiện như sau:

• Hàm số f (x) xác định trên khoảng (a, b) cho trước.
• a là một điểm thuộc khoảng (a, b) ban đầu.
• Trong trường hợp x tiến dần và có thể bằng a, ta nói hàm số f (x) ban đầu liên tục tại a.

Dạng 2: Hàm số liên tục tại khoảng

Nếu hàm số cho trước f(x) liên tục với mọi giá trị a bất kỳ tại khoảng (a, b) cho trước. Ta có thể nói rằng, hàm f (x) liên tục trên đoạn (a, b). Tuy nhiên, hàm số liên tục trên khoảng phải được biểu diễn bởi nét liền và không ngắt quãng.

Dạng 3: Hàm số liên tục trên tập R

Dạng 3, hàm số liên tục trên R được coi là trường hợp đặc biệt của dạng 2, hàm số liên tục trên khoảng. Nếu hàm số f(x) cho trước liên tục trên R thì với mọi giá trị thuộc R, hàm số f(x) cũng liên tục, gọi là liên tục trên khoảng.

Trong đó, có một số hàm luôn luôn liên tục trên R là: y = sin a, y = cos a, hàm phân thức có tập xác định ban đầu là R và các hàm mũ.

Như vậy, kiến thức về hàm số liên tục trong chương trình lớp 11 đã được gói gọn trong bài viết trên. Hy vọng những kiến thức trên đây hữu ích đối với bạn.

Có thể bạn quan tâm: Cấp số nhân là gì? Định nghĩa, công thức và bài tập ứng dụng