Thể tích hình trụ được tính như thế nào? Lưu ý gì khi tính thể tích hình trụ?

Trong toán học không gian, người học đã rất quen thuộc với các loại hình như hình cầu, hình chóp,... Bên cạnh đó là các công thức tính diện tích và chu vi của mọi loại hình. Bài viết dưới đây chúng tôi sẽ chia sẻ công thức tính thể tích hình trụ và những thông tin có liên quan. Cùng tham khảo ngay nhé.
Nội dung bài viết[Hiển thị]
Hình trụ là gì?
Hình trụ là một hình khối đơn giản gồm có hai mặt. Bao gồm mặt đáy hình tròn song song và bằng nhau. Hình trụ có giao tuyến gồm 2 mặt phẳng vuông góc với trục của nó.
Để tính thể tích hình trụ thì có công thức như sau:
V = S.h = π.r^2.h
Trong đó:
- S là diện tích của đáy hình trụ;
- h là chiều cao của hình trụ
- r là bán kính của đáy hình trụ
Tóm lại, thể tích hình trụ được tính bằng chiều cao nhân với diện tích đáy. Các dữ liệu về thể tích của hình trụ cho biết vật đó có thể chiếm được bao nhiêu phần trong không gian 3 chiều.
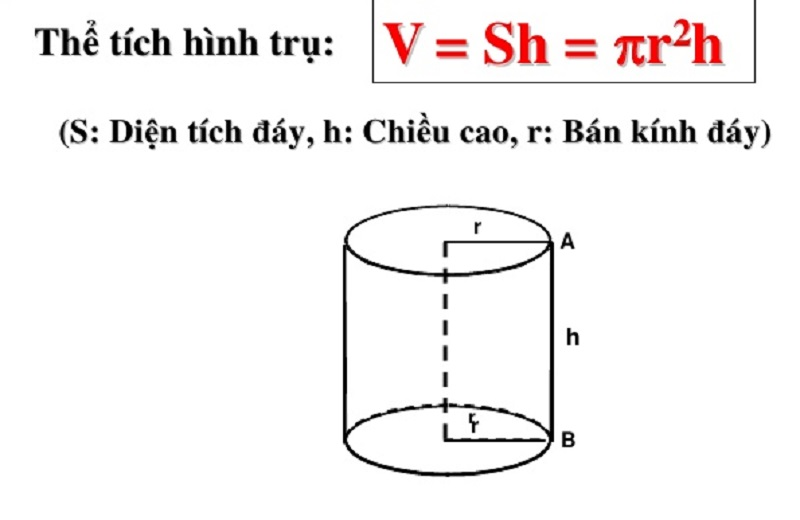
HÌnh trụ tròn xoay có thể tích bằng công thức chiều cao nhân với diện tích của đáy. Bán kính của mặt đáy bất kỳ là r và chiều cao của hai mặt đáy là h. Vì vậy công thức tính thể tích hình trụ tròn là: V = π.r^2.h hoặc A = 2π.r.h
Trong đó:
- V tức là thể tích hình trụ
- r là bán kính hình trụ
- h là chiều cao của hình trụ
- π xấp xỉ bằng 3,14
- A là diện tích hình trụ
Có thể bạn quan tâm: Tìm hiểu khái niệm, dấu hiệu nhận biết và cách tính diện tích hình bình hành
Làm sao để tính được thể tích hình trụ?
Có thể thấy mọi người sẽ nhìn thấy hình trụ thường xuyên nhưng để tính được thể tích thì không phải ai cũng nắm rõ. Ở trên chúng tôi đã cung cấp cho bạn đọc công thức tổng quát về các tính thể tích của hình trụ. Tuy nhiên để tính được thể tích hình trụ thì bạn đọc cần lưu ý những chi tiết như sau:
Cần tìm được bán kính của đáy
Có thể dựa vào các dữ liệu được cho để tính bán kính đáy. Nên đo khoảng cách rộng của mặt đáy được bao nhiêu, sau đó chia cho hai sẽ ra bán kính của đáy. Ví dụ như khoảng cách rộng của mặt đáy bằng 5 thì bán kính của mặt tròn đáy là 5/2 = 2.5 cm.
Lưu ý, đường kính của dây cung lớn nhất trong một hình tròn. Vì vậy khi đo độ dài đường kính cần phải chọn một mép đường nằm ở điểm số 0 của thước đo, để có thể có số liệu chính xác nhất. Sau đó đo phần độ dài lớn nhất mà không lấy mốc số 0 để có thể tìm ra được độ dài của đường kính.
Cần tính diện tích đáy tròn
Sau khi đã biết được bán kính của mặt đáy thì có thể tính diện tích theo công thức là S = π.r^2
Ví dụ: Cho bán kính mặt đáy bằng 2.5. Hãy tính diện tích của đáy tròn:
Trả lời:
Dựa vào công thức đã cho, ta có: A = π.2,5^2
A = π.6,25. Vì số π = 3,14 nên ta được diện tích hình tròn là 19,63cm2
Cần tính chiều cao của hình trụ
Để tính chiều cao của hình trụ, có thể dùng thước đo khoảng cách của 2 mặt đáy tròn. Trong một số trường hợp có thể bài đã cho sẵn đường chéo đến viền hình tròn. Từ dữ liệu trên bạn đọc có thể tính được chiều cao cụ thể của hình trụ. Nên áp dụng định lý pitago để tính chiều cao.
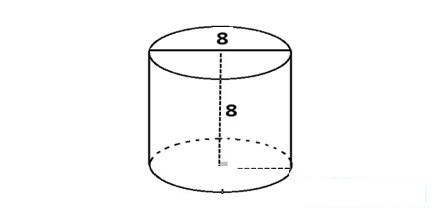
Ví dụ: Tính thể tích hình trụ biết đường kính đáy bằng độ cao của hình trụ d = h = 8 cm.
Giải: Vì đề bài cho đường kính (ký hiệu là d) của mặt đáy nên các bạn chỉ cần chia giá trị này cho 2 để được bán kính r vì d = 2r.
➩ r = 8 : 2 = 4 cm.
Áp dụng công thức tính thể tích ta có:
V= πr28 = π428 = 128π
Vậy thể tích hình trụ là 128π (cm3) hay ∼402 cm3
Có thể bạn quan tâm: Cách tính chu vi hình tròn và các bài tập ví dụ về tính chu vi hình tròn
Một số lưu ý khi tính thể tích hình trụ
Khi tính thể tích của hình trụ cần thống nhất đơn vị tính về cùng một đơn vị. Đơn vị thể tích luôn phải là mũ lập phương. Thể tích của các hình dạng lập phương sẽ bằng diện tích mặt đáy nhân với chiều cao của vật đó. Đối với việc đo kích thước của đường kính hình tròn sẽ là khoảng cách lớn nhất giữa hai điểm của hình tròn đó.

Ví dụ: Tính thể tích hình trụ biết bán kính mặt đáy r = 4 cm; chiều cao hình trụ h = 8 cm.
Trả lời: Các bạn chỉ cần áp dụng công thức tính thể tích:
V = πr^2h
Ta có: V= π4^2.8 = 101cm3
Vậy thể tích hình trụ là 101 (cm3)
Công thức tính thể tích hình trụ không quá khó. Tuy nhiên bạn đọc nên áp dụng thường xuyên để không quên công thức. Bài viết trên là những thông tin có liên quan đến thể tích hình trụ. Hãy tiếp tục theo dõi thêm nhiều bài viết hay ho nữa tại web ReviewAZ nhé.
Có thể bạn quan tâm: Các kiến thức cần nắm vững về đường trung trực có thể bạn chưa biết
Có thể bạn quan tâm!
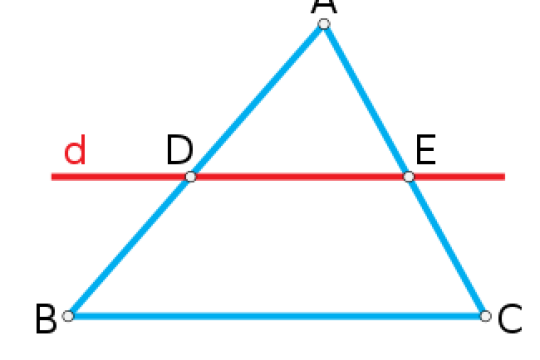
Định lý talet là gì? Ứng dụng định lý Talet vào toán học như thế nào?
Định lý Pitago hay định lý định lý Fermat đã vô cùng quen thuộc trong lĩnh vực toán học rồi. Nhưng bạn đã từng nghe...

Big data là gì? Tính ứng dụng của big data trong cuộc sống hiện nay
Công nghệ hay phần mềm truyền thống không thể xử lý dữ liệu trong một thời gian nhất định mang lại hiệu quả không cao....

0987 là mạng gì? Sim số 0987 mang ý nghĩa gì hay không?
Các cặp số như 88 hay 86 được xem là có phong thủy tốt. Vậy số mạng 0987 thì sao? Hãy cùng tìm hiểu xem...

Debit note là gì? Các cách trình bày debit note phổ biến nhất hiện nay
Vậy khi tìm kiếm thông tin về lĩnh vực này, bạn đã bao giờ nghe đến khái niệm debit note là gì chưa? Cùng tìm...

Baking soda là gì? Những công dụng không thể bỏ qua của baking soda
Baking soda là một trong những nguyên liệu rất thường gặp trong nấu nướng. Ngoài ra, nhiều người còn ưu tiên sử dụng sản phẩm...

PMS là gì? PMS có ứng dụng như thế nào trong kinh doanh khách sạn?
Kinh doanh khách sạn cần những gì để tồn tại trong thị trường cạnh tranh? Để thành công, khách sạn cần có đặt phòng trực...


