Bảng Công Thức Nguyên Hàm đầy đủ nhất gồm cơ bản - mở rộng

Toán học luôn là một lĩnh vực vô cùng thú vị và cũng rất phức tạp, với nhiều công thức khác nhau. Một trong số những kiến thức toán đóng vai trò quan trọng nhất, đó chính là công thức nguyên hàm. Hệ thống nguyên hàm luôn khiến người học cảm thấy băn khoăn và khó hiểu. Vì thế, bài viết sau đây của ReviewAZ sẽ hỗ trợ bạn giải đáp các thắc mắc về định nghĩa, tính chất và công thức tính cụ thể. Hãy cùng tham khảo ngay nhé!
Nội dung bài viết[Hiển thị]
Định nghĩa nguyên hàm
Nguyên hàm là một vấn đề quan trọng trong bộ môn giải tích. Quá trình tìm kiếm nguyên hàm còn được gọi với cái tên khác là tích phân bất định. Bất kỳ hàm số liên tục nào nằm trên đoạn hoặc khoảng từ a tới b đều tồn tại nguyên hàm.

Ta có định nghĩa cụ thể về công thức nguyên hàm như sau:
Bài toán cho một hàm số f xác định trên K. Hàm số F này sẽ được gọi là nguyên hàm của hàm số f trên K trong trường hợp F(x) khả thi trên K và đáp ứng được điều kiện: F'(x) = f(x) với mọi x thuộc K.
Toán học chứng minh được rằng mọi hàm số liên tục trên K đều có nguyên hàm trên K.
Định lý và tính chất của nguyên hàm bạn cần biết
Bất kỳ công thức toán học nào đều tồn tại định lý và tính chất riêng. Điều này giúp cho người học dễ dàng áp dụng vào các bài toán thực tế, cũng như phân biệt giữa các công thức với nhau. Định lý và tính chất nguyên hàm được thể hiện như sau:
Định lý nguyên hàm
- Định lý 1: Trong trường hợp F(x) đóng vai trò là một nguyên hàm của f(x) trên K, thì các hằng số C và hàm số G(x)= F(x)+ C sẽ là nguyên hàm của f(x) trên K
- Định lý 2: Trong trường hợp F(x) là nguyên hàm của f(x) trên K, mọi nguyên hàm của F(x) trên K sẽ đều có dạng F(x)+C. Điều kiện cần và đủ là C là một hằng số
Tính chất nguyên hàm
Về mặt tính chất, nếu f(x) và g(x) đều là hai hàm số chạy liên tục trên K, ta sẽ có tính chất sau:
- Tính chất 1:
∫f’(x)dx= f(x)+ C
- Tính chất 2: ∫k.f(x)dx= k.∫f(x)dx trong điều kiện k là số thực khác 0
- Tính chất 3: ∫[f(x) + hoặc - g(x0]dx= ∫f(x)dx + hoặc - ∫g(x)dx
Có thể bạn quan tâm: Cách tính diện tích hình thang giúp cho việc học tập trở nên thuận lợi
Công thức tính nguyên hàm đơn giản
Tính nguyên hàm luôn là một thách thức lớn đối với các bạn học sinh. Bởi để giải quyết một phép tính, bạn sẽ cần liên hệ rất nhiều kiến thức khác nhau một cách hệ thống và bài bản. Nếu muốn chinh phục bộ môn này dễ dàng hơn, hãy áp dụng các phương pháp dưới đây:
Phương pháp tính nguyên hàm
Có hai phương pháp tính nguyên hàm phổ biến nhất:
- Cách 1: Phương pháp biến đổi biến số
Nếu ∫f(u)du= F(u) +C, u=u(x) và có đạo hàm chạy liên tục. Ta có cách tính: ∫f[u(x)].u’(x)dx= F[u(x)]+C
- Cách 2: Phương pháp từng phần
Nếu hàm số u=u(x) và v=v(x) có đạo hàm nằm trên K chạy liên tục, ta có
∫u(x).v’(x)dx= u(x).v(x)- ∫u’(x).v(x)dx
Hoặc: ∫u.dv= u.v- ∫v.du
Bảng công thức tính nguyên hàm
Việc sử dụng thành thạo bảng nguyên hàm có vai trò vô cùng quan trọng. Nếu ghi nhớ được các công thức này, bạn sẽ dễ dàng chinh phục được mọi phép toán trong quá trình học hoặc đề thi.
- Cơ bản
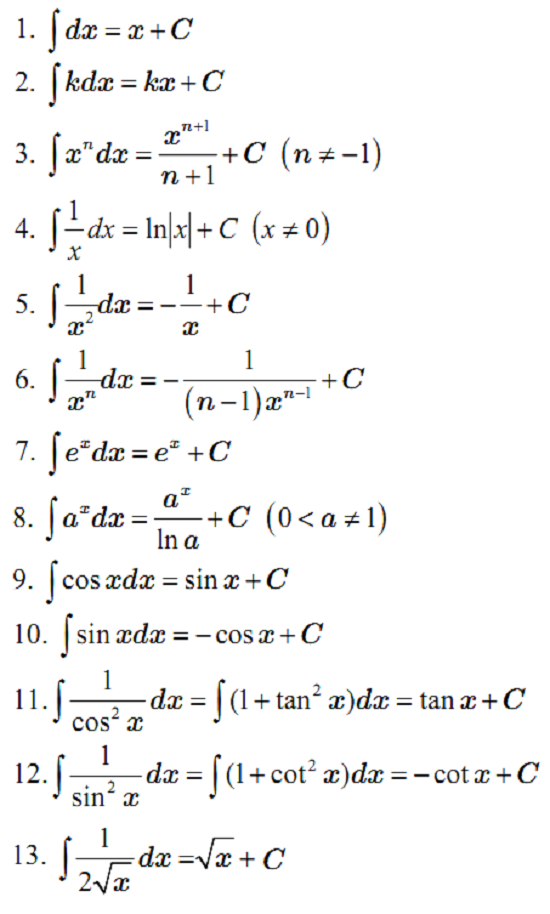
- Mở rộng:
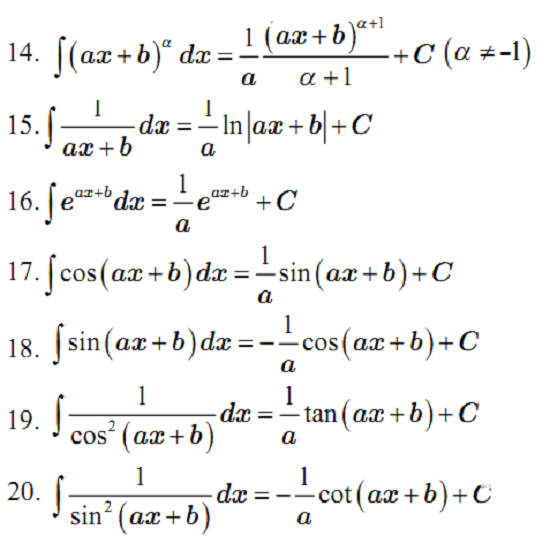
- Nâng cao

Có thể bạn quan tâm: Cách tính chu vi hình tròn và các bài tập ví dụ về tính chu vi hình tròn
Cách chinh phục công thức nguyên hàm nhanh chóng nhất
Nguyên hàm nằm trong danh sách những vấn đề Toán học quan trọng, được ứng dụng thi cử thường xuyên. Việc học thuộc và áp dụng công thức cần rất nhiều chăm chỉ và nỗ lực. Thế nhưng không phải chỉ cần áp dụng công thức là ta có thể tìm ra biến số của nguyên hàm. Do đó, ngay từ hiện tại, bạn cần lên kế hoạch để chinh phục công thức nguyên hàm thật nhanh chóng và đơn giản nhất.
Các bước bạn nên áp dụng đó là:
- Trang bị cho mình đầy đủ kiến thức về đạo hàm, vi phân, biết phân biệt đạo hàm sơ cấp, đạo hàm thứ cấp của hàm hợp
- Không nhầm lẫn giữa các công thức hàm lượng giác khác nhau
- Ghi nhớ thật kỹ bảng nguyên hàm
- Luyện tập, ứng dụng giải quyết các bài toán theo từng cấp độ. Trước khi bắt tay vào giải, bạn cần xác định đây là hàm gì, có những ẩn số gì và phải giải quyết theo từng bước ra sao, áp dụng công thức nào
- Ghi chép công thức và các ví dụ cụ thể
- Bắt đầu với các bài toán đơn giản, sau đó tiến dần lên nâng cao để cải thiện trình độ
Chìa khóa vàng chinh phục nguyên hàm luôn là sự chăm chỉ, cẩn thận và tỉ mỉ. Vì thế, nếu bạn mong muốn sở hữu một số điểm cao môn Toán, hoặc vượt qua kỳ thi quan trọng, thì cần áp dụng đầy đủ các bước trên.
Vậy là chúng ta đã cùng tìm hiểu công thức nguyên hàm phổ biến nhất trong môn Toán. Nếu cảm thấy bài viết hữu ích, đừng quên theo dõi và cập nhật thêm nhiều thông tin từ ReviewAZ nhé!
Có thể bạn quan tâm: Cấp số nhân là gì? Định nghĩa, công thức và bài tập ứng dụng
Có thể bạn quan tâm!
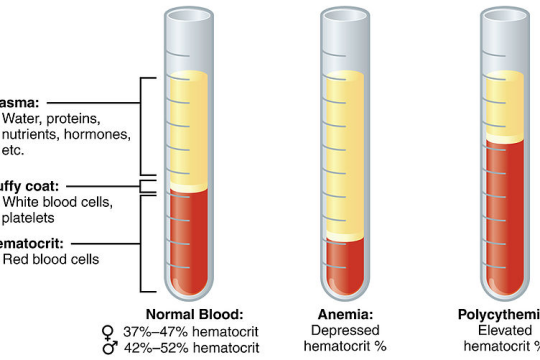
Hematocrit là gì? Chỉ số bao nhiêu là bình thường?
Hematocrit là thuật ngữ thuộc ngành y học. Khi bạn đi khám và kiểm tra sức khỏe định kỳ, được chỉ định xét nghiệm máu,...

Con giáp thứ 13 là con gì? Cách nhận biết con giáp thứ 13 xung quanh bạn
Trong thời gian gần đây, chủ đề về “ con giáp thứ 13” đang xuất hiện rất nhiều trên mạng xã hội. Đây cũng là...

Layout là gì? Một số quy tắc cần chú ý trong thiết kế Layout
Với những người thường xuyên tham gia vào thiết kế, đặc biệt thiết kế website chắc chắn không còn quá xa lạ với từ layout....

Thẻ ghi nợ là gì? Lợi ích của thẻ ghi nợ như thế nào?
Thẻ ghi nợ là loại thẻ được sử dụng rất nhiều để thanh toán hầu hết các mặt hàng hiện nay.Trong bài viết này hãy...

Maintain là gì? Cách phân biệt maintain với những từ đồng nghĩa
Là một từ vựng khá quen thuộc và được sử dụng phổ biến, tuy nhiên từ maintain vẫn khiến chúng ta hay nhầm lẫn với...
Anti Hbs là gì? Mục đích của việc xét nghiệm Anti Hbs?
Sức khỏe là mối quan tâm lớn nhất đối với tất cả mọi người. Trong các dịch vụ chuyên khoa y tế thì việc xét...


